What does it mean to compute something? We often associate it with math but computation is actually about symbol manipulation. A “computer” basically takes an input, applies some rules to it and outputs something. For centuries, the “computers” were humans whose job was to perform tedious calculations.
Then in 1930s, David Hilbert asked 3 questions, one of them was the Entscheidungsproblem(the Decision Problem), which asks — Is there a mechanical process that can decide if any given mathematical statement is true or false? To answer this, mathematicians had to first define what a “mechanical process” actually was.
What Is a Turing Machine?
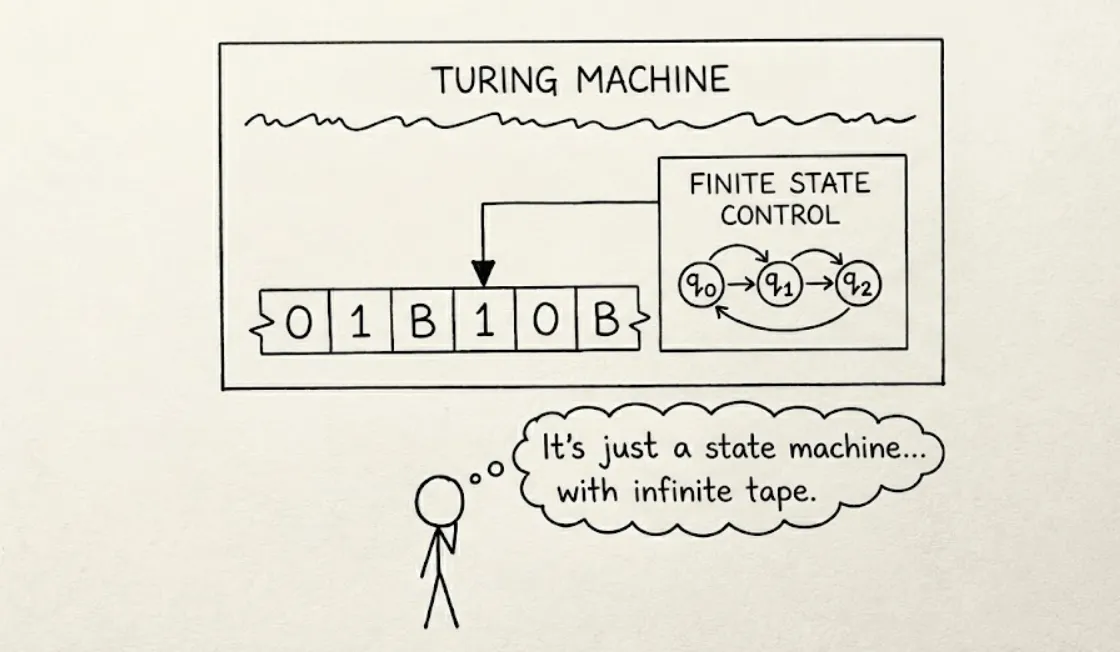
Alan Turing provided the most famous answer to the above question. He imagined a theoretical device, now called as a turing machine, that could simulate any logic. It consists of —
- An infinite tape - divided into squares, each containing a symbol (like 0 or 1)
- A read/write head - that can move left or right, read a symbol and change it
- A state table - A set of instructions telling the machine what to do
Turing proved that if a problem can be solved by a human following a set of instructions, it can be solved by this simple machine. This simple machine also became the blueprint for every computer we use today.
Adding 1 on a turing machine
Let’s add 1 to 1011 (which is 11 in decimal).
The algorithm: (for x + 1 (where x is in binary))
- Go to the rightmost digit of x
- If it’s 0, flip it to 1 and stop
- If it’s 1, flip it to 0 and move left (carry the 1)
- Repeat until you find a 0 or run out of digits
Initial: [1] 0 1 1 _ (start)
1 [0] 1 1 _ (go to the rightmost digit...)
1 0 [1] 1 _
1 0 1 [1] _
1 0 1 1 [_] (hit blank, turn around)
1 0 1 [1] _ (1 → 0, carry 1)
1 0 [0] 0 _ (1 → 0, carry 1)
1 [1] 0 0 _ (0 → 1, done!)
Result: 1100 (which is 12)The Church-Turing Thesis
At roughly around the same time, Alonzo church developed lambda calculus, a formal system in mathematical logic for expressing computation based on function abstraction and application.
Turing’s approach was “mechanical” (focused on moving parts), Church’s was “functional” (focused on mathematical rules). They eventually proved that these two systems were logically equivalent. This discovery is known as Church-Turing Thesis, which states that anything that can be “computed” can be computed by a Turing machine.
Turing Completeness
A system is considered “Turing complete” if it can perform any calculation that a human or a computer could ever logically do, given it has enough time and memory. It means you can use this system to simulate any other computer or programming language. The 3 requirements for a system to be turing complete are —
- Maintain state (memory) - it must be able to store data and retrieve it later (like variables or a “tape”)
- Make Decisions - it must have if/then logic
- Repeats (loops or recursion) - it must be able to do something over and over until a condition is met
Most modern programming languages (Python, C++, Java) are Turing-complete but there are also some strange things that accidentally meet those three requirements:
- SQL (with recursion)
- PowerPoint (yes, someone proved this with animations and hyperlinks+)
- Excel Formulas (Modern Excel formulas (specifically with
LAMBDA) can perform any computation.) - Minecraft redstone circuits (Players have built functional CPUs)
- Magic: The Gathering (Researchers proved that a specific, complex setup of cards can simulate a Turing machine)
- Conway’s Game of Life
If a system is Turing complete, it inherits a famous problem.
The Halting Problem
Turing proved that some problems are undecidable — no algorithm can solve them.
Implications:
- No compiler can detect all infinite loops
- No debugger can perfectly analyze all code
- Some questions have no algorithmic answer
This isn’t “we haven’t figured it out yet.” It’s “mathematically impossible”.
Alan Turing
Alan Turing (1912–1954):
- Defined computability (1936)
- Broke the Enigma code in WWII
- Pioneered artificial intelligence (the Turing test)
- Contributed to mathematical biology
He was prosecuted for homosexuality in 1952, chemically castrated, and died in 1954. He was 41. Tragic, I know. In 2013, Queen Elizabeth II granted a posthumous pardon. In 2019, his face appeared on the £50 note.
His abstract machine laid the foundation for the digital age.
The Takeaway
A tape, a head, some states, and rules. That’s it. Yet this simple abstraction:
- Defines what computation means
- Proves what’s impossible to compute
- Unifies all programming languages
- Inspired modern computer architecture
Every program you run is instructions executing on a very fancy Turing machine. Your RAM is the tape. Your CPU is the head. Your code is the transition function.